This page is devoted to the Happy Cube, aka Wirrel Warrel-kubus in Dutch. The Happy Cube® was designed by Belgian inventor Dirk Laureyssens in 1986. They are elegantly simple, yet quite addictive. For a detailed description of the Happy Cube, follow one or more of the links below.

While playing around with the individual 6 piece cubes, and some attempts for combinations and such, it became known that you could make a large cube with double-length edges by using pieces from differently-coloured mats. The large cube requires 24 pieces, whereas I only had 30 at the time, which corresponded to all but the purple mats. Of course, 30 is still more than 24, but with only 6 pieces to spare this would become a hard job.

Luckily I managed to find a solution by combining the 5 other colours (in 1990). This is a scan from my solution on paper:

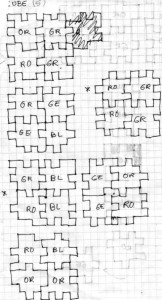
Paper solution (1990)

The top left image displays a schematic layout for the 5-colour, 24 pieces cube. Jürgen Köller really helped speeding up the layout drawing process. If you happen to have other solutions for a 5-colour large cube please let me know.

The bottom left picture shows a different, recently found 5-colour solution. I was sent proof that a solution for 4-colour, 24 pieces cube does not exist (this involves counting the “teeth” on the sides of the pieces). Both Willem Siemelink (February 1st, 2003) and Michael Kiermaier (22 February, 2003) composed a similar calculation. A 1-colour, six pieces cube (1×1) has exactly 8 corner positions filled. 4 Coloured mats therefore provide 32 filled corner positions, but a 2x2x2 cube has only room for 26.

This articles was published in Cursor, Eindhoven University’s weekly newspaper:

Newspaper scan (1990)

I have not been able to contact the photographer, so the photograph is used with permission from the newspaper only.

If I manage to find some time I want to add some more discussion on the Happy Cube and the logic behind solutions; of course there is a lot of trial-and-error and exhaustive search to working with Happy Cubes. This does not directly imply that there is less mathematics to it than, for instance, Rubik’s Cube. Willem Siemelink also sent me an (unpublished) Happy Cube solver that makes it easy to generate solutions, for instance 2x2x2 cubes with monochromatic sides, as done by Jan Verbakel.